Хотя не совсем весь: не без ссылок на другие страницы.
Главная страница.
Написать мне письмо.

Булева Алгебра для школьника и студента технического вуза (это — персональный сайт руководителя некоего математического кружка).

                                           ... и пусть, интересующийся Булевой Алгеброй, НАРОД
                                  всегда помнит интересующий его адрес booleanalgebra.narod ... 
                                                    ... и пусть следит за обновлениями этого сайта ...

                          Мои ученики и мои выпускники — школьники старших классов и студенты технических вузов. Это пособие я составляю для своих подопечных. Они, в подавляющем большинстве, — не теоретики, а практики. Им не нужны тонкости и подробности того, что такое Алгебра вообще и что такое Булева Алгебра в частности.  Как будущих инженеров, их больше должны интересовать основы исчисления высказываний.
                           Но как вводить понятие высказывания? Дать его, как фундаментальное понятие, а потом ввести кучу аксиом? Можно и так. Только я напомню о том, что как было сказано выше, я являюсь руководителем математического кружка для старших школьников, а мои выпускники-студенты технических вузов. Тонкости и теоретические дебри им не нужны. Поэтому, с Вашего позволения, я буду излагать материал в "кружковой" традиции. Кого интересует нечто большее, тем советую начать пока с малого.
**************************************************************************
**************************************************************************
**************************************************************************
        (С Вашего позволения, для обозначения определения 
           я буду использовать значок def)
           Итак, поехали ...

                                            Основные понятия

def Высказыванием называется повествовательное предложение, о котором можно однозначно сказать, истинно оно, или ложно.
                     Примечание: когда мы производим алгебраические операции над высказываниями, 
                     мы  абстрагируемся от содержания высказываний, нас интересуют только их значения.
def Говорят, что высказывание имеет значение "логическая единица", если он истинно.
def Говорят, что высказывание имеет значение "логический нуль", если он ложно.
def Конъюнкцией, или логическим умножением, или логически "И" называется такая операция над высказываниями, которая двум высказываниям A и B сопоставляет такое высказывание C, истинность которого (или значение которого) определяется следующей таблицей :
A B C
0 0 0
0 1 0
1 0 0
1 1 1

Обозначение : 
 

C= A&B=A*B (В последнем случае используется точка умножения, т.е.тот же значок, что и для арифметического умножения)

Примечание : допустимо точку умножения пропускать, как в арифметике.

def Дизъюнкцией, или логическим сложением, или логически ""ИЛИ" (соединительным)" называется такая операция над высказываниями, которая двум высказываниям A и B сопоставляет такое высказывание C, истинность которого (или значение которого) определяется следующей таблицей :
A B C
0 0 0
0 1 1
1 0 1
1 1 1

Обозначение : 


C=A+B=                             A символ "птичка" B

def Инверсией или негацией, или логическим отрицанием, или логически "НЕ" называется такая операция над высказываниями, которая одному высказыванию A сопоставляет такое высказывание B, истинность которого (или значение которого) определяется следующей таблицей :
A B
0 1
1 0

Обозначение: 

                B=     символ "кочерга" A=     "A с крышкой"

Примечание к определению операции логического отрицания :
Её результат имеет так же название "инверсное значение переменного".
ДАМЫ И ГОСПОДА! При первом чтении можно от этого синего текста  прокатиться вниз  следующему синему тексту!

                                         Переключательные функции

                                                                                      При первом чтении зелёный текст
                                                                                       можно пропустить.

def Переключательной функцией называется такая функция от нескольких аргументов, все аргументы которой являются высказываниями, и значение которой также является высказыванием.
Переключательная функция однозначно задаётся своей таблицей истинности :
Общий принцип заполнения таблицы истинности :
X1 X2      ...      Xn-1 Xn       F (X1, X2,…,Xn)
 0   0       ...       0   0  F(0,0,...,0,0)
 0   0       ...       0   1  F(0,0,...,0,1)
 0   0       ...       1   0  F(0,0,...,1,0)
......................
1 1      ...      1 1 F(1,1,...,1,1)
Верхняя строка называется шапкой таблицы.
          Крайний правый столбец, за исключением первой позиции. называется столбцом значений.
           Все остальные позиции в таблице, за исключением, как я уже сказал, самой верхней строки и самого правого столбца, называются телом таблицы. В теле таблицы перебираются всевозможные значения аргументов функции.
              Шапка и тело одинаковы для всех таблиц истинности при фиксированном значении n, т.е. для всех переключательных функций от n аргументов.
           Чтобы создать переключательную функцию от n аргументов, надо от балды заполнить стобец значений. Произвольно!!! Вот и всё!!!
              В шапке таблицы истинности переключательной функции от n аргументов перечисляются все её аргументы (в заголовках первых n столбцов) и, наконец, само имя функции F (X1, X2,…,Xn).
Тело таблицы заполняется всеми возможными строками, начиная от строки из всех нулей, заканчивая строкой из всех единиц. Каждая строка, как это даже самому пьяному ежу понятно, представляет собой двоичную запись своего порядкового номера, если условится считать, что начальная строка имеет нулевой номер. Алгоритм заполнения тела таблиц-это циклический алгоритм, в котором навьючено друг на друга n циклов. Быстрее всего изменяется переменная Xn, помедленнее Xn-1, а всего медленнее - X1. Как ВЫ знаете уже из Комбинаторики, если имеется n вложенных циклов, в которых каждая переменная пробегает ровно k значений, то такой цикл срабатывает ровно k в степени n раз.В теле таблицы истинности должно быть, таким образом, 2 в степени n строк, а последняя строка представляет собой двоичную запись числа (2 в степени n) минус1.
Столбец значений для каждой функции индивидуален и неповторим (в смысле целиком неповторим). Это-её анкетные данные (проводили когда-нибудь анкетирование?). Ну, это было лирическое отступление. А теперь-опять к делу!

                                    Переключательные функции от двух аргументов

      Все существующие на свете логические функции двух переменных можно представить в виде таблицы, которая строится следующим образом:
      Берётся обычная таблица истинности для функции двух переменных:

Таблица истинности для функции двух аргументов. Общий вид

      И кладётся эта таблица на левый бок в буквальном смысле этого слова:

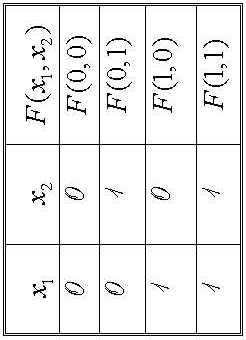
Таблица лежит на левом боку

      после чего столбец значений заполняется всеми возможными значениями. Какими значениями? Нулями и единицами! Позиций в столбце значений всего четыре, значит, способов заполнить его всеми возможными различными значениями 24=16 штук. Эти способы очень удобно нумеровать от 0 до 15, т.к. самый первый способ заполнения столбца значений — это просто четыре нуля, а последний способ заполнения столбца значений — это просто четыре единицы. Напомним, что четыре нуля (или вообще любое количество нулей) — это нуль, а четыре единицы — это 15 в двоичной системе счисления.
      Учитывая всё вышесказанное, мы и обозначим эти функции соответственно:

Обозначения для функций

      А теперь представим их в виде таблицы:

Таблица лежит на левом боку Тяните
линейку прокрутки
вниз
и
смотрите,
как это
остроумоно!
№  F(0,0) F(0,1) F(1,0) F(1,1) Что за функция ? Как функцию обозначаем?
 0   0  0  0  0   Тождественный нуль
или
Тождественная ложь 		Тождественный нуль
 1   0  0  0  1   Конъюнкция,
или
Логическое "И"
или
Логическое умножение 		Конъюнкция
 2   0  0  1  0   Отрицание импликации Отрицание импликации
 3   0  0  1  1   X1 X1
 4   0  1  0  0   Отрицание обратной импликации Отрицание обратной импликации
 5   0  1  0  1   X2 X2
 6   0  1  1  0   Функция Жигалкина,
или
Сложение по модулю 2,
или
Разделительное "ИЛИ"
или
отрицание эквиваленции 		Функция Жигалкина
 7   0  1  1  1   Дизъюнкция,
или
Соединительное "ИЛИ"
или
Логическое сложение 		Дизъюнкция
 8   1  0  0  0   Функция Пирса,
или
Стрелка Пирса
или
отрицание дизъюнкции 		Функция Пирса
 9   1  0  0  1   Эквиваленция
или
Равносильность 		Эквиваленция
10   1  0  1  0   Отрицание X2 Отрицание X2
11   1  0  1  1   Обратная импликация Обратная импликация
12   1  1  0  0   Отрицание X1 Отрицание X1
13   1  1  0  1   Импликация
или
Следствие 		Импликация
14   1  1  1  0   Функция Шеффера,
или
Штрих Шеффера
или
отрицание конъюнкции 		Функция Шеффера
15   1  1  1  1   Тождественная единица,
или
Тождественная истина
или
Тавтология 		Тождественная единица

     Позже мы разберём отдельно каждую из этих функций, напишем для неё уравнения.
 
 

                                Логические базисы

    Этот темнокрасный текст при первом чтении 
                                                                                      можно пропустить.
           А теперь дадим важное определение из другой оперы:
def Композицией, или суперпозицией функций называется функция, получаемая подстановкой значений одних функций в качестве аргументов в другие функции.
def Логическим базисом или базисом на множестве всех переключательных функций называется такое множество переключательных функций, что любую другую переключательную функцию можно представить, как суперпозицию функций данного множества.
Теорема. Множество функций : КОНЪЮНКЦИЯ, ДИЗЪЮНКЦИЯ, ИНВЕРСИЯ образуют базис на множестве всех переключательных функций от n аргументов при любом натуральном n. 

Доказательство

Примечание:
Я  старался  изложить 
доказательство  так , 
чтобы пьяному ёжику 
было понятно.   Но для 
более  непонятливых 
сделаю  потом  !!! 
ЖДИТЕ НА САЙТЕ !!!
             Пусть имеется некоторая произвольная переключательная функция F(X1,X2,...,Xn)
от n аргументов, где n- произвольное натуральное число.
             Введём понятие  элементарная конъюнкция-конституэнта единицы следующим образом:
def  Элементарной конъюнкцией-конституэнтой единицы для переключательной функции F(X1,X2,...,Xn) называется  логическое произведение, составляемое по следующему алгоритму: 
1. Найти в столбце значений таблицы истинности переключательной функции F(X1,X2,...,Xn) позицию, в которой стоит единица.
2. Выписать в строчку все аргументы переключательной функции.
3. На те аргументы, которым  в  строке тела таблицы истинности соответствующей позиции столбца значений, выбранной в пункте 1, соответствуют нули, надеть крышки (знак логического отрицания), а те аргументы, которым в  строке тела таблицы истинности соответствующей позиции столбца значений, выбранной в пункте 1, соответствуют единицы, оставить без отрицания.
4. Между аргументами с крышками без крышек, полученными в пункте 3, поставить знак логического произведения
             Такое логическое произведение для переключательной функции F(X1,X2,...,Xn) всегда существует хотя бы одно, если в теле таблицы истинности переключательной функции F(X1,X2,...,Xn)  есть хотя бы одна единица.

Рассмотрим два случая :

1.В теле таблицы истинности переключательной функции F(X1,X2,...,Xn)  есть 
хотя бы одна единица.
        Рассмотрим, как выглядит столбец значений таблицы истинности самой 
элементарной конъюнкцией-конституэнтой единицы, как тоже некоторой переключательной функции:
            В той позиции тела таблицы, которая соответствует выбранной в пункте 1 позиции столбца значений функции F(X1,X2,...,Xn), эта самая конституэнта единицы будет иметь единицу, т.к. аргументы без крышек, полученные в пункте 3,  равны единицы; а все аргументы с крышками, полученные в пункте 3, равны нулю, но они станут также  равны единице после надевания крышек. А как известно из моего пособия (см. ссылку Основные понятия  ), конъюнкция логических единиц равна логической единице.
            В любой другой позиции тела таблицы, которая не соответствует выбранной 
в пункте 1 позиции столбца значений функции F(X1,X2,...,Xn), эта самая конституэнта единицы будет иметь нуль, т.к. либо не все аргументы без крышек, полученные в пункте 3,  равны единицы; либо не все аргументы с крышками, полученные в пункте 3, равны нулю, и, стало быть, они станут также  равны единице после надевания крышек. логических единиц. А как известно из моего пособия (см. ссылку Основные понятия  ), конъюнкция будет равна логическому нулю, если не все её операнды равны логической единице.
        Таким образом столбец значений таблицы истинности самой 
элементарной конъюнкцией-конституэнтой единицы, как тоже некоторой переключательной функции, выглядит так:
                                          -единица в той позиции, которая выбрана в пункте 1.
                                          -нули во всех остальных позициях.
        А теперь рассмотрим, как выглядит столбец значений таблицы истинностидизъюнкции всех таких элементарных конъюнкций-конституэнт единицы, как тоже некоторой переключательной функции:
             Как известно из моего пособия (см. ссылку Основные понятия  ), дизъюнкция будет равна логическому нулю, если все её операнды равны логическому нулю. Значит, на тех позициях, где сама функцияF(X1,X2,...,Xn)имеет в столбце значений логический нуль, дизъюнкция всех таких элементарных конъюнкций-конституэнт единицы, будет иметь так же логический нуль, ибо ни одна такая конституэнта единицы не была построена по той позиции, в которой функция F(X1,X2,...,Xn) имеет в столбце значений логический нуль (напоминаю читателю, что в в пункте 1 мы выбирали в столбце значений таблицы истинности функции F(X1,X2,...,Xn) позицию, в которой стоит единица!).
             Как известно из моего пособия (см. ссылку Основные понятия  ), дизъюнкция будет равна логической единице, если хотя бы один её операнд равен логическоой единице. Значит, на тех позициях, где сама функцияF(X1,X2,...,Xn)имеет в столбце значений логическую единицу, дизъюнкция всех таких элементарных конъюнкций-конституэнт единицы, будет иметь так же логическую единицу, ибо хотя бы одна такая конституэнта единицы была построена по той позиции, в которой функция F(X1,X2,...,Xn) имеет в столбце значений логическую единицу (напоминаю читателю, что в в пункте 1 мы выбирали в столбце значений таблицы истинности функции F(X1,X2,...,Xn) позицию, в которой стоит единица!).

        Таким образом столбец значений таблицы истинности дизъюнкции всех таких элементарных конъюнкций-конституэнт единицы, как тоже некоторой переключательной функции, выглядит так:
                                          -единица в тех позициях, в которых функция F(X1,X2,...,Xn) имеет единицу;
                                          -нуль в тех позициях, в которых функция F(X1,X2,...,Xn) имеет нуль.

        Таким образом столбец значений таблицы истинности дизъюнкции всех таких элементарных конъюнкций-конституэнт единицы, совпадает со столбцом значений таблицы истинности самой функции F(X1,X2,...,Xn) !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
              А что значит, что столбцы значений двух  переключательных функций совпадают? Да то и значит, что эти две функции равны! Вот и всё !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
             Таким образом, функция F(X1,X2,...,Xn) равна дизъюнкции всех своих элементарных конъюнкций-конституэнт единицы, а значит мы получили для неё выражение в виде композиции функций "КОНЪЮНКЦИЯ", "ДИЗЪЮНКЦИЯ" и "ИНВЕРСИЯ" !!!
2.В теле таблицы истинности переключательной функции F(X1,X2,...,Xn)  нет
ни одной единицы.
             Значит, функция F(X1,X2,...,Xn) равна нулю. Логический нуль также является некоторой   композицией функций "КОНЪЮНКЦИЯ", "ДИЗЪЮНКЦИЯ" и "ИНВЕРСИЯ" от аргументов X1,X2,...,Xn :  например, 0= (X1+X2+...+Xn)*0. 
            Таким образом, и в случае 2.мы так же получили для функции F(X1,X2,...,Xn) выражение в виде композиции функций "КОНЪЮНКЦИЯ", "ДИЗЪЮНКЦИЯ" и "ИНВЕРСИЯ" !!!

            Таким образом, произвольная переключательная функция F(X1,X2,...,Xn)
от n аргументов, где n- произвольное натуральное число, может быть представлена в виде композиции функций "КОНЪЮНКЦИЯ", "ДИЗЪЮНКЦИЯ" и "ИНВЕРСИЯ"  !!!
             Значит, множество функций "КОНЪЮНКЦИЯ", "ДИЗЪЮНКЦИЯ" и "ИНВЕРСИЯ" образуют логический базис (см.  определение логического базиса по этой ссылке  ). 

Что и требовалось доказать!!!

А теперь эту штуку умесно обозвать именем какого-то такого

логического базиса:
ВНИМАНИЕ !!! Очень важное определение !
def Универсальным логическим базисом, называется множество функций : КОНЪЮНКЦИЯ, ДИЗЪЮНКЦИЯ, ИНВЕРСИЯ.
А теперь снова вернёмся к нашим баранам :

Свойства функций универсального логического базиса

                 Да по-просту говоря-это свойства уже известных нам ранее КОНЪЮНКЦИИ, ДИЗЪЮНКЦИИ, и ИНВЕРСИИ. Вот и всё!
          ДАМЫ И ГОСПОДА! Все, кто при первом чтении перематывал линейку прокрутки от синего текста вниз к следующему синему тексту, уже домотались до цели! Дальше можете не мотать!
    Важное примечание :
Все нижеследующие формулы справеливы
для любых высказываний A, B и C.
Спешу заметить, что все эти формулы можно доказать! Доказать математически!
     А. Свойства логического сложения и умножения, совпадающие с соответствующими свойствами соответствующих арифметических операций :
                                                     


С позволения читателя, чтобы 
                                                                                не загромождать статью кучей вставленных
                                                                                рисунков, я буду символ умножения 
                                                                                заменять звёздочкой.

1. Коммутативность логического сложения :
            A+B=B+A
/От слова «коммутация»-переключение/.
2. Коммутативность логического умножения :
            A*B=B*A

3. Ассоциативность логического сложения : 
            (A+B)+C=A+(B+C)
/От слова «ассоциация»-объединение/.
4. Ассоциативность логического умножения : 
             (A*B)*C=A*(B*C)

5. Наличие нейтрального элемента для логического сложения :
             0+A=A –левый нейтральный элемент
             A+0=A –правый нейтральный элемент 
(т.к. левый и правый нейтральный элемент совпадают, то он просто называется нейтральным элементом)
6. Наличие нейтрального элемента для логического умножения :
             1*A=A –левый нейтральный элемент
             A*1=A –правый нейтральный элемент 
(т.к. левый и правый нейтральный элемент совпадают, то он просто называется нейтральным элементом)

7. Мультипликативное свойство логического нуля :
             0*A=0 –левое мультипликативное свойство
             A*0=A –правое мультипликативное свойство
(т.к. левое и правое мультипликативное свойство имеют место одновременно, то оно просто называется мультипликативным свойством)

8. Дистрибутивность логического умножения относительно логического сложения :
             A*(B+C)=A*B+A*C –левая дистрибутивность
             (B+C)*A=B*A+C*A –правая дистрибутивность
(т.к. левая и правая дистрибутивность имеют место одновременно, то она просто называется дистрибутивностью) 
/Кто такой дистрибьютор? –Это посредник!/.

ПРИМЕЧАНИЕ: 
КОЕ-КАКИЕ СВОЙСТВА ЭТИХ ФУНКЦИЙ МОЖНО ИЗЛОЖТЬ БОЛЕЕ КРАТКО.
ТЕХ, КОГО НЕ ИНТЕРЕСУЕТ КРАТКОЕ ИЗЛОЖЕНИЕ, ПРОСИМ ПРОКАТИТЬСЯ ПО ТЕКСТУ ВНИЗ.
ОСТАЛЬНЫЕ МОГУТ ПРОЧИТАТЬ СЛЕДУЮЩИЕ СТРОКИ:

1. Коммутативность логического сложения :
            A+B=B+A
/От слова «коммутация»-переключение/.
2. Коммутативность логического умножения :
            A*B=B*A

3. Ассоциативность логического сложения : 
            (A+B)+C=A+(B+C)
/От слова «ассоциация»-объединение/.
4. Ассоциативность логического умножения : 
             (A*B)*C=A*(B*C)

5. Наличие нейтрального элемента для логического сложения :
             0+A=A+0=A

6. Наличие нейтрального элемента для логического умножения :
             1*A=A*1=A 

7. Мультипликативное свойство логического нуля :
             0*A=A*0=0

8. Дистрибутивность логического умножения относительно логического сложения :
             A*(B+C)=A*B+A*C 
             (B+C)*A=B*A+C*A 

     Б. Свойства логического сложения и умножения, несовпадающие с соответствующими свойствами соответствующих арифметических операций :

1. Дистрибутивность логического сложения относительно логического умножения :
     (B*C)+A=(B+A)*(C+A) –левая дистрибутивность
     A+(B*C)=(A+B)*(А+C) –правая дистрибутивность
(т.к. левая и правая дистрибутивность имеют место одновременно, то она просто называется дистрибутивностью)

Прошу обратить внимание на то, что для логических сложения и умножения справедливы обе (!!!) дистрибутивности,  т.е. не только дистрибутивность умножения относительно сложения, но и дистрибутивность сложения относительно умножения. /Обратите внимание на пункты А.8 и Б.1./

         Однако не следует путать два вида одной и той же дистрибутивности (т.е. правую и левую в пункте Б.1.) с двумя дистрибутивностями разных видов (т.е. умножения относительно сложения и сложения относительно умножения).

2. Отсутствие понятия аддитивного обратного элемента, 
т.е. обратного элемента по операции сложения :
НЕВЕРНО, что для любого высказывания A существует высказывание (-A), такое, что:
     A+(-A)=0, или (-A)+A=0.
3.  Отсутствие понятия мультипликативного обратного элемента, т.е. обратного элемента по операции  умножения :
НЕВЕРНО, что для любого высказывания A существует высказывание A (-1), такое, что:
     A*A (-1)=1, или A (-1)*A=1.
4. Необратимость логического сложения, т.е. 
НЕВЕРНО, что для любых высказываний A и C существует высказывание B, такое, что:
     A+B=C.
5. Необратимость логического умножения, т.е. 
НЕВЕРНО, что для любых высказываний A и C существует высказывание B, такое, что:
     A*B=C.
6. Дублироваие слагаемого в логической сумме не изменяет значения логической суммы:
        A=A+A=A+A+A=A+A+A+A=A+A+...+A
7. Дублироваие сомножителя в логическом произведении не изменяет значения логического  произведения:
        A=A*A=A*A*A=A*A*A*A=A*A*...*A
8. Законы поглощения  :
     A*(A+B)=A
     A+(A*B)=A

ПРИМЕЧАНИЕ: 
КОЕ-КАКИЕ СВОЙСТВА ЭТИХ ФУНКЦИЙ МОЖНО ИЗЛОЖТЬ БОЛЕЕ КРАТКО.
ТЕХ, КОГО НЕ ИНТЕРЕСУЕТ КРАТКОЕ ИЗЛОЖЕНИЕ, ПРОСИМ ПРОКАТИТЬСЯ ПО ТЕКСТУ ВНИЗ.
ОСТАЛЬНЫЕ МОГУТ ПРОЧИТАТЬ СЛЕДУЮЩИЕ СТРОКИ:
 

1. Дистрибутивность логического сложения относительно логического умножения :
     (B*C)+A=(B+A)*(C+A) 
     A+(B*C)=(A+B)*(А+C) 

Прошу обратить внимание на то, что для логических сложения и умножения справедливы обе (!!!) дистрибутивности,  т.е. не только дистрибутивность умножения относительно сложения, но и дистрибутивность сложения относительно умножения.

2. Отсутствие понятия аддитивного обратного элемента, 
т.е. обратного элемента по операции сложения :
НЕВЕРНО, что для любого высказывания A существует высказывание (-A), такое, что:
     A+(-A)=0, или (-A)+A=0.
3.  Отсутствие понятия мультипликативного обратного элемента, т.е. обратного элемента по операции  умножения :
НЕВЕРНО, что для любого высказывания A существует высказывание A (-1), такое, что:
     A*A (-1)=1, или A (-1)*A=1.
4. Необратимость логического сложения, т.е. 
НЕВЕРНО, что для любых высказываний A и C существует высказывание B, такое, что:
     A+B=C.
5. Необратимость логического умножения, т.е. 
НЕВЕРНО, что для любых высказываний A и C существует высказывание B, такое, что:
     A*B=C.
6. Дублироваие слагаемого в логической сумме не изменяет значения логической суммы:
        A=A+A=A+A+A=A+A+A+A=A+A+...+A
7. Дублироваие сомножителя в логическом произведении не изменяет значения логического  произведения:
        A=A*A=A*A*A=A*A*A*A=A*A*...*A
8. Законы поглощения  :
     A*(A+B)=A
     A+(A*B)=A

     Б. Свойства операций логического отрицания

1. Закон двойного отрицания :

2. Законы де Моргана :
               –“отрицание конъюнкции есть дизъюнкция отрицаний” :

               –“отрицание дизъюнкции есть конъюнкция отрицаний” :

3. Закон склеивания :

 

4. Тождественный нуль :

5. Тождественная единица :

Минимизация логических (переключательных) функций

      На этом сайте мы опишем два приёма минимизации логических функций: минимизации логических функций:
1. Преобразование логических выражений посредством использования законов логических операций.
2. Минимизация с использованием карт Карно. 

Примечание по первому методу:
      Пусть дано некоторое логическое выражение в универсальном логическом базисе. Тогда мы действуем с этим выражением следующим образом:
- используем все те законы для раскрытия скобок и приведения подобных слагаемых, которые нам известны из курса арифметики, работая с логическим умножением и логическим сложением так же, как мы умеем это делать с соответствующими арифметическими операциями;
- вспоминаем о том, что для логических сложения и умножения справедливы обе дистрибутивности, т.е. не только дистрибутивность умножения относительно сложения, но и дистрибутивность сложения относительно умножения;
- вспоминаем законы поглощения и склеивания;
- вспоминаем о том, что если для выполнения тех или иных действий нам необходимо добавить слагаемое в логическую сумму ещё раз, то сумма от этого не изменится, или если необходимо добавить сомножитель в логическое произведение, то произведение от этого не изменится;
- действуем везде так, как подсказывает наша интуиция и наш жизненный опыт.
          Следует отметить, что первый метод требует от человека определённой математической интуиции. Успех зависит от того, насколько развита у Вас эта интуиция. Научить человека действовать этим методом невозможно, можно только помочь научиться. Это- как стихи писать. Через некоторое время я просто приведу несколько примерчиков по использованию этого метода.  Ждите!!!Следите за обновлениями! А пока примерчиков нет, предлагаю читателю порешать самостоятельно упражнения для самоконтроля.
Относительно второго метода:
               Второй метод не требует такой развитой математической интуиции, как первый. Этот метод достаточно просто алгоритмизуем. Существуют программы, позволяющие минимизировать логические функции при помощи карт Карно. Но у него есть большой недостаток: эти карты существуют лишь для переключательных функций от трёх-четырёх аргументов. Если аргументов больше, то надо уже как-то хитрить, т.е. применять Ваш жизненный опыт и математическую интуицию. "Кромсайте" Вашу функцию от пяти аргументов и более на функции, состоящие из четырёх и менее аргументов, а уже потом только минимизируйте! Как это сделать- сами смотрите!
             Что касается применения карт Карно для минимизации логических функций от четырёх и менее аргументов, то страница на эту тему уже создана на моём сайте. У неё пока (временно) есть один недостаток, который впоследствии будет обязательно устранён. Это её несколько большой объём относительно других страниц (61 килобайт). Потому она не так быстро загружается. Пока изложение материала на этой странице идёт целым куском. Потом оно будет разбито на отдельные маленькие смысловые кусочки, и каждый кусочек займёт отдельную страничку. Но уже появилась отдельная страничка, содержащая целый кусок, посвящённый одному только примеру на применение карт Карно. Впоследствии изложение будет усовершениствовано. Появятся и другие примеры. Ждите!

 Продолжение следует.
Всё ещё впереди.                            А хотите наверх?

Hosted by uCoz