Пример №1 (первая отдельная страничка с примером).


		Главная страница.
		Минимизация логических функций.
		Карты Карно.
		Напишите мне: booleanalgebra@narod.ru

Данная страничка без рисунков не воспринимается!!!
Пример №1
(Будем считать, что примерчики, разобранные на другой странице, имели номера (-1)и нуль.
Эта страничка у меня - пока первая отдельная страничка, содержащая отдельный пример. )

Имеется некоторая логическая функция F(X1,X2,X3,X4), заданная своей картой Карно (напоминаем, что карта Карно – это такой же однозначный способ задания функции, как и таблица истинности):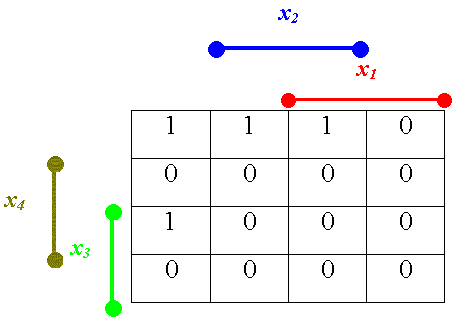

               Для этой функции необходимо составить формулу в универсальном логическом базисе.
               Как мы будем это делать?
               А вот, как:
               Нужно рассмотреть все единички, стоящие в табличке, определить, в областях истинных значений каких логических выражений они стоят, и просуммировать эти выражения.
               Итак, с чего мы начнём?
               Правильно! Рассмотреть все единички, стоящие в табличке! Их у нас четыре. Но для того, чтобы, определить, в областях истинных значений каких логических выражений они стоят, мы должны будем как-то их разделить, разгруппировать (с тем, чтобы потом уже просуммировать выражения). Как будем их разделять? Первое, что приходит в голову, это рассмотреть отдельно три “дружественных” единицы и одну отдельную “гордо-стоящую”.

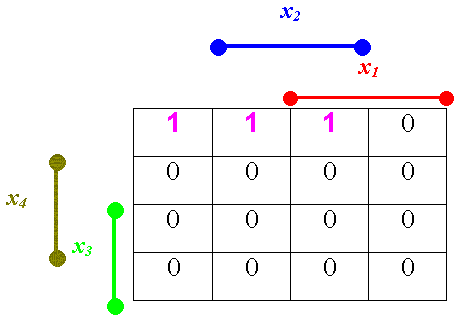
Три дружественных единицы

              В области истинных значений какого логического выражения стоят три подруги? Сразу скажем, что не может это логическое выражение быть просто логическим произведением, оно непременно должно являться суммой логических произведений.
               А почему оно произведением быть не может? Да потому, что всякое произведение аргументов (или их отрицаний) имеет область истинных значений, являющуюся пересечением областей истинных значений для аргументов (или их отрицаний). А если каждая из областей истинных значений для какого-либо аргумента (или его отрицания) есть полоса шириной в две клетки, занимающая ? всей таблицы, а пересечения етих самых областей значений являются областями, занимающими ?, 1/8, или 1/16 всей таблицы (что составляет соответственно 4, 2 и 1 клеток для произведений второго, третьего и четвёртого рангов; произведение первого ранга, т.е. сам аргумент или его отрицание, имеет область истинных значений, состоящую из восьми клеток).
                Поэтому трёх подруг мы разобьём на … две пары (по две подруги в каждой! итого 2+2=3).

Единицы верхняя левая и средняя

Объединяем верхнюю левую и среднюю единицы. В области истинных значений какого логического выражения они находятся? Как составить это логическое выражение?

              Для составления сего логического выражения будем перебирать все аргументы функции F:
x1   примет участие в составлении сего выражения, очевидно, с отрицанием, ибо рассматриваемая парочка единичек полностью лежит в области истинных значений для не x1 ;
x2   вообще не будет принимать участия в составлении этого выражения, ибо одна из этих единиц лежит в области истинных значений для   x2, а другая единичка лежит в области истинных значения для   не x2;
x3   примет участие в составлении сего выражения, очевидно, с отрицанием, ибо рассматриваемая парочка единичек полностью лежит в области истинных значений для    не x3;
x4   примет участие в составлении сего выражения, очевидно, с отрицанием, ибо рассматриваемая парочка единичек полностью лежит в области истинных значений для    не x4.

Таким образом, достопочтенные ДАМЫ И ГОСПОДА, вышеупомянутые две единички лежат в области истинных значений для выражения:

Единицы верхняя средняя и правая
Объединяем верхнюю среднюю и правую единицы. В области истинных значений какого логического выражения они находятся? Как составить это логическое выражение?

            Для составления сего логического выражения будем перебирать все аргументы функции F:
x1   вообще не будет принимать участия в составлении этого выражения, ибо одна из этих единиц лежит в области истинных значений для x1 , а другая единичка лежит в области истинных значения для   не x1 ;
x2   примет участие в составлении сего выражения, очевидно, без отрицания, ибо рассматриваемая парочка единичек полностью лежит в области истинных значений для   x2;
x3   примет участие в составлении сего выражения, очевидно, с отрицанием, ибо рассматриваемая парочка единичек полностью лежит в области истинных значений для    не x3 ;
x4   примет участие в составлении сего выражения, очевидно, с отрицанием, ибо рассматриваемая парочка единичек полностью лежит в области истинных значений для    не x4 .

Подводя итоги всего вышесказанного, будем иметь:
три верхние единицы лежат в области истинных значений выражения:

Может возникнуть вопрос: “Откуда взялась операция «плюс» (она же – логическое сложение или дизъюнкция)?”. Ответ очень прост: давайте рассмотрим не функцию F(X1,X2,X3,X4), а некоторую другую функцию H(X1,X2,X3,X4), которая задаётся следующей картой Карно:

в которой, как мы видим, в трёх рассматриваемых клеточках стоят единички, а в остальных – нули. Применим для функции H(X1,X2,X3,X4) эту самую нашу теорему. Что мы будем иметь?
Некоторая функция от четырёх аргументов H(X1,X2,X3,X4) задана своей картой Карно (см. выше). Имеется некоторое множество логических выражений:
G1(X1,X2,X3,X4) =

G2(X1,X2,X3,X4) =

таких, что:
1. В области истинных значений каждого из этих логических выражений в карте Карно, которой задана функция H(X1,X2,X3,X4), стоят единицы.
2. Во всех клетках карты Карно, которой задана функция H(X1,X2,X3,X4), не принадлежащих области истинных значений ни одной из этих функций, стоят нули.
Тогда для функции H(X1,X2,X3,X4) справедлива следующая формула:

H(X1,X2,X3,X4) =
= G1(X1,X2,X3,X4) + G2(X1,X2,X3,X4) =
= + =

А я о чём говорил? Теперь понятно, откуда взялся знак «плюс»?

Приступим же, наконец, к одинокой гордо-стоящей единице!

Одинокая гордая единица

Вот она, гордая, одинокая, важная:

         Где она находится? В области истинных значений для какого логического произведения? Как определить сомножители для этого логического произведения? Для того, чтобы определить сомножители для этого логического произведения, переберём все аргументы функции F:
x1   примет участие в составлении сего произведения, очевидно, с отрицанием, ибо рассматриваемая единичка полностью лежит в области истинных значений для не x1 ;
x2   примет участие в составлении сего произведения, очевидно, с отрицанием, ибо рассматриваемая единичка полностью лежит в области истинных значений для   не x2;
x3   примет участие в составлении сего произведения, очевидно, без отрицания, ибо рассматриваемая единичка полностью лежит в области истинных значений для    x3;
x4    примет участие в составлении сего произведения, очевидно, без отрицания, ибо рассматриваемая единичка полностью лежит в области истинных значений для   x4.

Подведём итоги:
Три дружные единицы стоят в области истинных значений для логического выражения:

Одинокая гордо-стоящая единица занимает область истинных значений логического выражения:

Какой научный вывод? Да такой, что для функция F справедливо (при всех значений её аргументов) следующая формула:
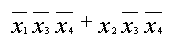F(x1,x2,x3,x4) =

Причем эта формула является тупиковой дизъюнктивной нормальной формой для функции F.

Конец примера 1.
наверх